A simple toy example of a three layered network:
Note 1: In order to view the 3D plots, mac users will need Xquartz installed (https://www.xquartz.org/).
require(igraph)
require(rgl)
#Another package that might be needed is "rglwidget". The function writeWebGL will show an error stating if rglwidget is required.
######################################////
######The basics######################////
######################################////
#1) Create a "food" network (three layers)
set.seed(432)
g1<-watts.strogatz.game(dim = 1,size = 5,nei = 2,p = .5,loops = FALSE,multiple = FALSE)
g2<-watts.strogatz.game(dim = 1,size = 10,nei = 2,p = .2,loops = FALSE,multiple = FALSE)
g3<-watts.strogatz.game(dim = 1,size = 30,nei = 1,p = .5,loops = FALSE,multiple = FALSE)
g123=g1+g2+g3
#Create more edges btw layers
g123=rewire(g123,each_edge(prob=.4,loops = FALSE,multiple = FALSE))
ne=15;add_edges(g123,edges = cbind(sample(1:vcount(g1),size = ne,replace = TRUE), sample((vcount(g1)+1):vcount(g123),size = ne,replace = TRUE)))#top layer
ne=30;add_edges(g123,edges = cbind(sample((vcount(g1)+1):(vcount(g1)+vcount(g2)),size = ne,replace = TRUE), sample((vcount(g1)+vcount(g2)+1):vcount(g123),size = ne,replace = TRUE)))#second layer
#A quick plot of the graph
plot(g123,vertex.size=1,vertex.label.cex=0.02)
#Create 3d coordinates of the network layout
circpos=function(n,r=1){#Coordinates on a circle
rad=seq(0,2*pi,length.out=n+1)[-1];x=cos(rad)*r;y=sin(rad)*r
return(cbind(x,y))
}
#
lay=rbind(cbind(circpos(vcount(g1),r=1), runif(n = vcount(g1),-1,1)),
cbind(circpos(vcount(g2),r=2), runif(n = vcount(g2),6,7)),
cbind(circpos(vcount(g3),r=4), runif(n = vcount(g3),13,17))
)
#2d plot using the previous layout
plot(g123,vertex.size=5,vertex.label=NA,layout=lay[,c(1,3)])
plot(g123,vertex.size=1,vertex.label=NA,layout=lay[,c(1,2)])
#3D graph plot
#Add some colour to nodes and edges
nodecols=c(rep("red",vcount(g1)),
rep("blue",vcount(g2)),
rep("yellow",vcount(g3)))
edgecols=function(elist,cols,grouplist){
whatcol=rep(length(cols)+1,nrow(elist))
finalcol=whatcol
for(i in 1:nrow(elist)){
for(k in length(cols):1){
if( k * (length( intersect(elist[i,], grouplist[[k]]) ) > 0)){
whatcol[i]=min(whatcol[i], k )
}
}
finalcol[i]=cols[whatcol[i]]
}
return(finalcol)
}
#Open 3d viewer
rgl.open()
rglplot(g123, layout=lay,vertex.size=5,vertex.label=NA,vertex.color=nodecols,
edge.color=edgecols(elist=get.edgelist(g123,names = FALSE),cols=c("orange","green","pink"),grouplist=list(1:vcount(g1), (vcount(g1)+1):(vcount(g1)+vcount(g2)), (vcount(g1)+vcount(g2)+1):vcount(g123)) )
)
###Storing the plot in an html file###
dirfolder="..." #your dir
#rgl.open()#instead of rgl.open use open3d, in order to save the plot.
open3d()
rglplot(g123, layout=lay,vertex.size=5,vertex.label=NA,vertex.color=nodecols,
edge.color=edgecols(elist=get.edgelist(g123,names = FALSE),cols=c("orange","green","pink"),grouplist=list(1:vcount(g1), (vcount(g1)+1):(vcount(g1)+vcount(g2)), (vcount(g1)+vcount(g2)+1):vcount(g123)) )
)
#Fix the view
rgl.viewpoint(theta=90, phi=0)
#Save a static 2d image:
rgl.snapshot(paste(dirfolder,"a_png_pic_0.png",sep=""), fmt="png", top=TRUE)
#Save the plot in a .htlm file:
rglfolder=writeWebGL(dir = paste(dirfolder,"first_net3d",sep=""), width=700)
#The previous function should create a file called index.htlm inside the folder "first_net3d". By opening this file in a browser (with javascript enabled) the 3d plot will be displayed again.
#Also the following command will open the plot in the browser:
browseURL(rglfolder)
Note 2: In order to view the .htlm file javascript should be enabled in the browser. (Here is an example on how to do this for safari ).
Although not covered in the previous script, further options are available such as edge/vertex size and the ability to control independently each of the nodes and edges in the graph. Here is an example that makes more use of these options:





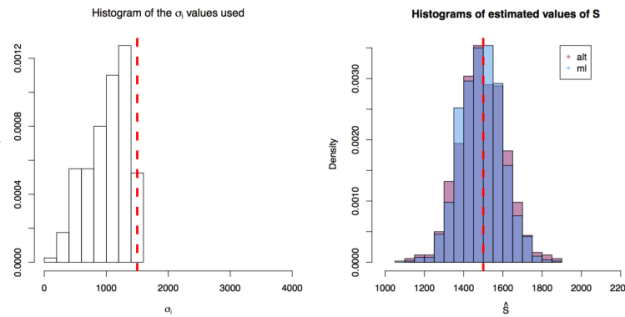 First simulation scenario where
First simulation scenario where 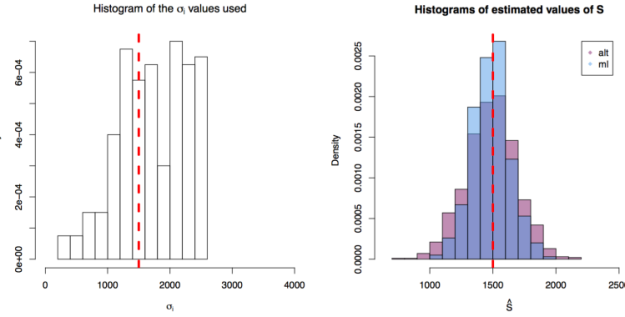 First simulation scenario where
First simulation scenario where  First simulation scenario where
First simulation scenario where 


 These network comparison statistics create frequency vectors of subgraphs and then compare these frequencies between the networks to obtain an idea of the similarity of the networks relative to their subgraph counts.
These network comparison statistics create frequency vectors of subgraphs and then compare these frequencies between the networks to obtain an idea of the similarity of the networks relative to their subgraph counts.








